Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
3.
Un disco cilíndrico de madera que pesa $45.0 \mathrm{N}$ y tiene un diámetro de $30.0 \mathrm{cm}$ flota sobre un cilindro de aceite cuya densidad es de $0.850 \mathrm{g/cm^{3}}$ como muestra la figura. El cilindro de aceite mide $75.0 \mathrm{cm}$ de alto y tiene un diámetro igual al cilindro de madera.
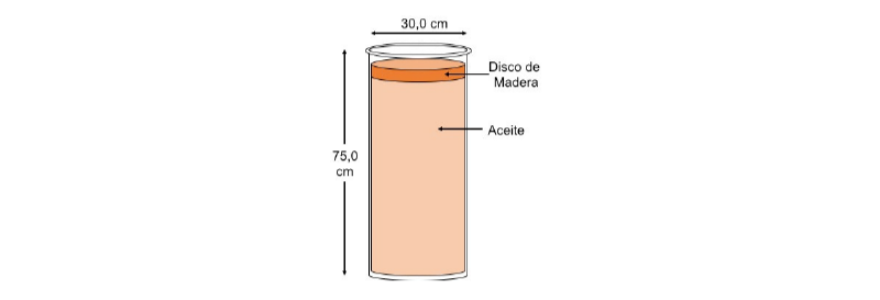
a) Calcule la presión manométrica en la parte superior de la columna de aceite.

a) Calcule la presión manométrica en la parte superior de la columna de aceite.
Respuesta
En este primer ítem queremos calcular la presión manométrica justo ahi donde te marqué:
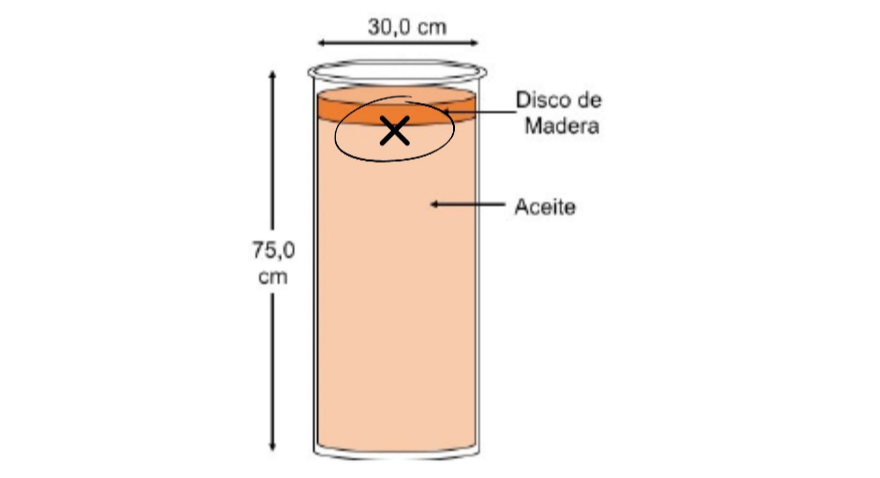
Reportar problema

Entonces, fijate que la presión manométrica ahí es debida al disco de madera, que está ejerciendo esta presión (P):
$P = \frac{F}{A}$
La fuerza (F) es justamente el peso del disco $(45 \text{ N})$ y el área (A) del disco la calculamos a la partir de la expresión del área del círculo, que es $\pi \cdot r^2$. En este caso, el diámetro del disco es $30 \text{ cm}$, o sea, $0.3 \text{ m}$; por lo tanto su radio es la mitad, $0.15 \text{ m}$.
Con lo cual, el área del disco es $\pi \cdot (0.15 \text{ m})^2$
Entonces, la presión manométrica en el punto pedido (justo abajo del disco de madera) es...
$P = \frac{45 \text{ N}}{\pi \cdot (0.15 \text{ m})^2} = 637 \text{ Pa}$
Si nos hubieran pedido la presión absoluta (en vez de la manométrica) tendríamos que haberle sumado la presión atmosférica.
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
